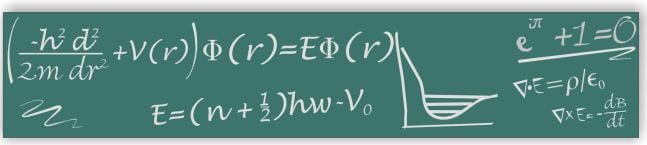
Leader: Prof. S. A. Rakitianski
Curriculum Vitae
Mr. P. Ogunbade, PhD (Pade Approximations for Extracting Resonace Parameters from Experimental Data)
Mr. P. Vaandrager, PhD (Application of the Jost-matrix theory in the analysis of some nuclear systems)
Ms. H. Fakira, MSc (Spectral points of non-Hermitial Hamiltonians)
Locating quantum resonances was always a difficult problem in quantum mechanics. The existing methods for theoretical description of resonant states in the few-body quantum systems are cumbersome and not universal. Our aim is to develop a unified approach that will allow us to obtain
the solution of the quantum mechanical problem using the same equations and the same method for bound, scattering, and resonant states.
Resonant states are formed when quantum objects (such as molecules or nuclei) collide at certain (resonant) energies. Before moving apart, they stay together for a while as a united complex. These intermediate quasi-stationary states (resonances) subsequently decay into various channels,
A+B → Resonance → C+D,
with different probabilities, and thus determine possible outcomes of the collision, i.e. the outcomes of a nuclear or a chemical reaction.
The concept of a quantum resonance (which is also called a quasi-stationary or quasi-bound state) emerged at later stages of the development of quantum mechanics. Attention to such states was drawn by George Gamow in his pioneering works on the alpha-decay. Over the years, nuclear physicists developed this idea to a rigorous mathematical concept and suggested various methods for locating resonances. These methods, however, are rather difficult and need to be adjusted for each particular physical process.
The role of quantum resonances in solid state and chemical physics was understood much later than in nuclear physics. Nowadays, it is clear that a full understanding of the properties of a quantum system and prediction of its behaviour cannot be achieved without knowing its spectrum, i.e. the energies of its bound states and resonances. This is true even in technological applications. For example, modern semiconductor devices, such as solid state lasers, based on nano-structures, cannot be properly designed without accurate treatment of various transitions among stationary and quasi-stationary states of the electrons and holes. In semiconductor nanostructures, the resonances are formed by charge carriers (electrons and holes) moving through the alternating nano-layers of different materials which are perceived by the charge carriers as a sequence of attractive wells and repulsive barriers.
In quantum chemistry, the resonating complexes can be formed when molecules collide with each other. Any chemical reaction occurs through molecular collisions. It is therefore very important to know at which energies and with which quantum numbers the resonances can be excited.
Going via an intermediate resonant state,
A+B → Resonance &→ C+D,
the rate of a particular reaction is either increased or decreased, or the reaction is diverted to a different channel, i.e. gives different final products. Undoubtedly, the ability to study and separate the contribution of each individual resonance into the whole reaction process would give us the power to change a chemical reaction process at our will by influencing the excitations of some of the inter-molecular resonances. The ability to analyze the resonance contribution to chemical reactions may therefore have a significant conceptual impact on chemistry, biology and even medicine. Identifying short-lived resonant intermediate states in a chemical reaction may, for example, make it possible to alter the outcome of a particular reaction by using fast laser pulses, which excite or de-excite the intermediate states and thereby alter the reaction outcomes.
Our approach is based on replacing the Schroedinger equation with an equivalent set of first order differential equations whose solutions asymptotically converge to the Jost functions (or Jost matrices in the multi-channel case). Within the current project, these solutions are constructed in the form of the power series near an arbitrary point on the Riemann surface of the energy. The expansion coefficients obey another (energy-independent) set of differential equations. This can be viewed as a generalization of the effective-range expansion.
Copyright © University of Pretoria 2025. All rights reserved.
Download the UP Mobile App